Calag Archive
Calag Archive
Dupuit-Forchheimer approximation may underestimate groundwater flow to San Joaquin River
Publication Information
California Agriculture 47(1):12-15.
Published January 01, 1993
PDF | Citation | Permissions
Abstract
Based on the commonly used Dupuit-Forchheimer approximation, estimates of groundwater contributions to flows in the San Joaquin River may be too low. Why? Because the vertical ground-water flows through the base of the channel have been neglected in estimates. Scientists found that flows have been underestimated by as much as 25%; such flows may degrade river water quality more than anticipated. The findings suggest the need to closely monitor subsurface runoff. A new look at the estimates is important to the development of water/salinity management plans.
Full text
For several years, as part of an analysis of the San Joaquin River's water quality, groundwater flow models were developed to measure the amount of groundwater entering the river along a 60-mile reach from Lander Avenue in Merced County to Vernalis in Stanislaus. Although groundwater flows to the river are relatively small, compared with the total river flows (California Agriculture, November-December 1987), their contributions of salt, boron, and other trace elements could be significant. Information about these contributions is needed to develop a basin water plan and water/salinity management plans.
In refining techniques used in the river water quality model, errors in estimating groundwater flow to the river were found and traced to an uncertainty in estimating monthly groundwater recharge to the land areas up to 2 miles distant on either side of the river, and correct parameterization of the hydraulic conductivity or permeability of the shallow groundwater zone. After improving our data base, we found that groundwater flow estimates, based on the Dupuit-Forchheimer (D-F) approximation, were consistently 5 to 50% lower than estimates made without using the approximation or than estimates based on U.S. Geological Survey (USGS) spot measurements along the river. For example, USGS mass balance estimates of groundwater flow based on surface flow measurements for river miles numbered 108 and 118 were 57 and 106 acre-feet per month, respectively, compared with 34 and 54 acre-feet per month for these locations, respectively, estimated from a D-F approximation based groundwater model.
Because of these discrepancies, we undertook a detailed study of the D-F approximation itself as it applies to estimating groundwater flows to rivers or unlined canals.
D-F approximation
In a discussion of the approximation in 1937, Morris Muskat of Gulf Research and Development Co. named it after both Dupuit and Forchheimer (French and German engineers, respectively, who independently developed this approximation to groundwater flows such that the governing differential equations could be solved analytically for practical drainage problems). He indicated that the approximation assumes that “for small inclinations of the free surface of a gravity-flow system, the streamlines can be taken as horizontal, and are to be associated with velocities which are proportional to the slope of the free surface, but are independent of the depth.” In other words, the D-F approximation assumes that all groundwater flow, or velocity, is in the horizontal direction only, and that the magnitude of this flow or velocity is proportional to the slope of the water table, or free surface. All vertical flows, or velocities resulting from infiltration and seepage, or the changing flow geometries resulting from geologic formations or water channels, are ignored because the slope of the water table is presumed to be mild. For steady, unconfined groundwater flow, the free surface is the streamline formed by a line connecting all locations of water at atmospheric pressure, that is, the water table. In essence, the D-F approximation neglects the vertical infiltration or recharge component of groundwater flow; as a result, it greatly simplifies the equations describing groundwater flow because it reduces the number of independent variables by one. Due to this simplification, all analytic solutions and most numerical solutions to these equations invoke the D-F approximation. (For 50-plus years, the D-F approximation has allowed solution of nearly all the drainage problems; the error in water table position was conservative compared to reality and the exact flow rates the approximation yielded were adequate to design drain pipe sizes and other drainage structures. Solutions without the approximation are difficult, can only be done numerically, and are not as easily coded.)
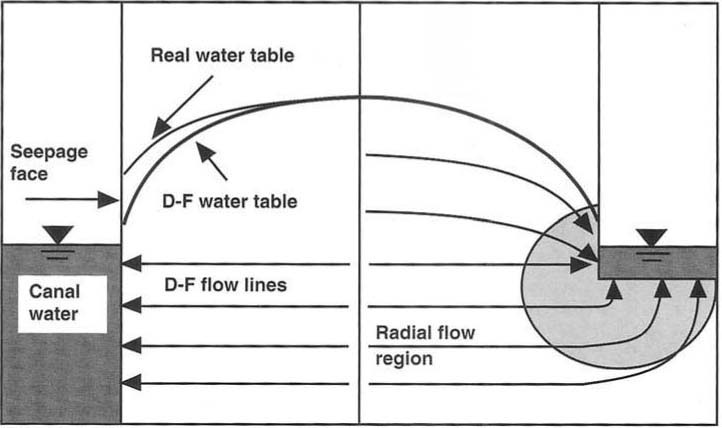
Many have shown, however, that the D-F approximation is internally inconsistent. For example, the approximation of horizontal streamlines implies (1) that vertical groundwater velocities are constant in the horizontal plane and (2) that when there are no-flow system boundaries (such as hydraulic divides, or bedrock formations in the vertical or near-vertical plane), vertical velocities are zero, vanishing across the entire domain — at this point the water table becomes horizontal. This conclusion directly contradicts the concept that flow is proportional to a sloping water table. Despite such inconsistencies, calculation of groundwater flow rate between two reservoirs fully penetrating to an impermeable layer using the D-F approximation is exact. However, the calculated position based on the D-F approximation of the water table is incorrect (fig. 1). Muskat concludes that success of the approximation is “a fortuitous coincidence rather than a reasonable approximation.”
The D-F approximation as applied to flow between two canals having different water levels leads only to an error in the water table position. However, in general, groundwater flows are at least a two-dimensional problem and both vertical and horizontal flows occur. Typically, vertical flows result from gravitational forces driving water into the soil, or from groundwater pressures (due to hydraulic connection to groundwater at higher elevations). Horizontal or lateral groundwater flows occur as groundwater at a slightly higher elevation flows to the lower elevation, that is “downhill.” In both cases, gravity is the primary driving force. For particular groundwater flow problems, some researchers have developed corrections for the vertical flow component neglected in the D-F approximation. This is especially true for design of subsurface drainage systems in which the radial flow (fig. 1) to the drain is accounted for by various “equivalent depth” correction equations. Others have modified the soil into fictitious layers, or developed an estimate of the error in water table position associated with the D-F approximation. For example, in 1972 Jacob Bear of the Israel Institute of Technology, Haifa, developed an equation for correcting the error in identifying potential energy associated with the force driving groundwater flow (a part of which is neglected in the D-F approximation). This error is approximately the same as the error in the water table position. The error may be quantified as
(Kh/Kv)i2 1+(Kh/Kv)i2where Kh and Kv are the horizontal and vertical conductivities of the soil, respectively, and i is the slope of the water table. In agricultural valleys, water table slopes are usually less than a few percent. Assuming a commonly encountered permeability ratio, (Kh/Kv), of 5 and a water table slope of 2%, the error in water table position associated with the D-F approximation is only 0.2%. Such an error is not practically possible to measure. The error approaches 5% for water table slopes as steep as 10% as may occur on hillslopes.
Fig. 1. Diagram of Dupuit-Forchheimer approximated water table, the real water table including the seepage face, and radial flow lines.
Corrections for limitations of the D-F approximation have been made for groundwater flow to drains, wells, below dams, and below islands. However, little work was found quantifying the error associated with applying the approximation towards estimation of groundwater flows to rivers or unlined canals. In the case of the San Joaquin River, which does not fully penetrate to the impermeable layer, this error may be substantial. The specific objective of this work then became to quantify the errors associated with the D-F approximation when applied to rivers (or canals) whose base does not extend in depth to a slowly permeable, or impermeable soil layer. Here, we illustrate types of errors that may be expected when applying the D-F approximation to estimating groundwater flows to a river.
Methods
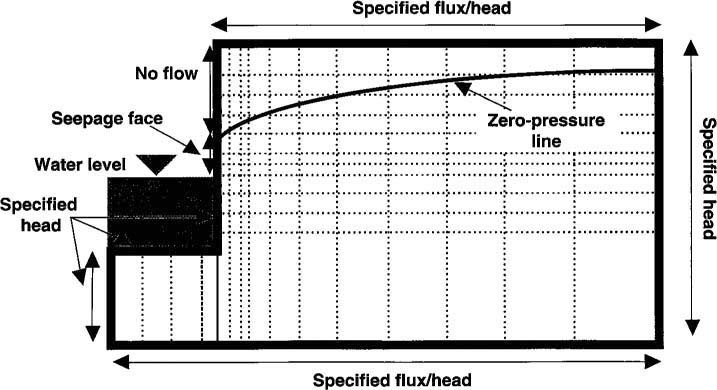
Numerical finite-difference solutions to the differential equations describing groundwater flow with and without the D-F approximation were developed to evaluate the effects of making, or using this approximation on calculations of water table position and groundwater contributions to river flows. Solutions based on the D-F approximation are widely available from both the public and private sector and are relatively simple. In contrast, solving the fundamental soil-water flow equation without the D-F approximation is relatively complex. For example, complete formulation of the nonD-F solution requires consideration of the unsaturated flow region to enable location of the water table by the model rather than by assigning its position beforehand as a boundary condition. In addition, the boundary conditions associated with the “seepage face” (the height of saturated soil having water at atmospheric pressure located just above the canal water surface for the lower water level canal, see figure 1) and space- and time-dependent fluxes are relatively complex, though probably more realistic. Computer codes were developed by the authors for both the D-F approximation solution and the variably saturated, nonD-F approximation solution.
We applied the numerical solutions to a grid layout schematically (fig. 2). We simulated the problem with different grid sizes, up to 2,500 nodes (nodes can be thought of as the points where the grid lines intersect; the greater the number of nodes, the more accurately the solution applies to the region, that is, the much finer the grid mesh). In order to optimize computer time, successively finer grid meshes were used until we found a negligible difference in solutions for water table position from one grid size to the next. This final grid we termed the “fine” grid size which was then used for the rest of the simulations. The same data base and boundary conditions (with the exception of the seepage face) were used in simulations based on solutions with and without the D-F approximation. Results from each pair of simulations were then compared.
Results
Using the models based on solutions with and without the D-F approximation, we evaluated the effects of average water table slope, permeability ratio (Kh/Kv), infiltration recharge, and canal, or riverbed geometry on the errors associated with the D-F approximation. The error was calculated in terms of percentage from
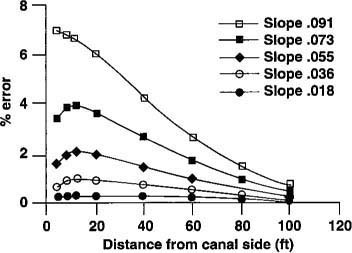
% error=No approx solut - D-F approx solut × 100% No approx solutA critical D-F assumption is that the slope of the zero-pressure line (water table) should be mild enough to minimize the vertical component of subsurface flow. Results (fig. 3) indicate that for an average water table slope of less than 2%, arbitrarily calculated at 60 feet from the canal, the overall error in its location (water table) is no more than 1%. As the water table slope increases, the error in the D-F water table location increases, especially near the canal side. The larger error is attributable to the increasing error associated with height of the seepage face. For results from the simulated scenario, an error of about 7% occurs at a distance only a few feet from the canal side, while an error of less than 1% results at distances in excess of 100 feet from the canal.
This difference in error is due to the different magnitudes of the water table slopes at both locations. Near the canal, the water table slope tends to be greater, resulting in vertical flows not accounted for in the D-F approximation. At the far side, the slope remains mild, allowing for mostly horizontal flow. The magnitude of percent error (fig. 3) is consistent with that given by the equation developed by Bear. As also indicated by the error equation of Bear, we found that as the permeability ratio increases, the error in the water table position, as given by the solution to the D-F equation, also increases. Generally, it seems that the error in water table position resulting from use of the D-F approximation in describing groundwater flow is practically insignificant for water table slopes of less than about 10%.
An alternative means of evaluating the effects of vertical flow on the error resulting from the D-F approximation is to consider the effect of infiltration recharge to the water table. As expected in this case, we found that increasing the steady vertical recharge to the water table in areas adjacent to the canal from 0.1 ft/day to 0.5 ft/day increased the percent error by a factor of 2.5 near the canal, a factor of approximately 2 at 60 feet from the canal and diminishing to near zero error at 120 feet from the canal.
Fig. 3. Effect of average water table slope on error in water table location due to the D-F approximation for a conductivity ratio (Kh/Kv = 3.
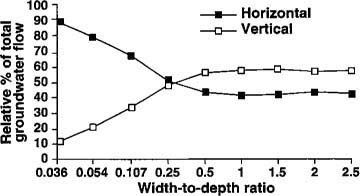
Fig. 4. Groundwater flow to a canal is affected by the ratio of the canal bed width to depth to an impermeable layer.
Having gained some experience and understanding of the errors in water table position associated with the D-F approximation, we turned our attention to the errors associated with groundwater flows to the canal or river. When simulating unconfined subsurface flow to a canal, it became apparent that the flow field was dominated by horizontal flow distant from the canal, shifting to a transition region of mixed vertical and horizontal flow nearing the canal, then finally a region of radial flow adjacent to the canal. We found that total groundwater flows to the channel depended on the ratio of the channel bed width to the depth of the impermeable layer underlying the canal. As canal or riverbed width increase, the error in estimating groundwater flow to the channel, based on the D-F approximation, increases because the region of radial flow through the base of the channel also increases in size.
Conversely, radial or vertical flow nears zero in the case of a very narrow canal bed width. In this case, subsurface flow enters the canal from horizontal streamlines that are mostly parallel to the impermeable layer. Figure 4 shows the vertical component of flow at near zero for a canal width of negligible size; the horizontal component has a value equivalent to that of the D-F approximation. The combined magnitude of vertical flows exceeds that of the horizontal contribution when the canal bed width reaches a significant size relative to the depth of the impermeable layer. This occurs as a result of an increase in canal perimeter or surface area that allows entry of both vertical flows from below and radial flows from the sides of the river. There is also a change in the energy status of the water just below the streambed. The lack of change in the values of both the vertical and horizontal flows at ratios greater than 0.5 (fig. 4) is due to a balancing effect of the forces driving flow which offset the effect of an increase in streambed width. The error in quantifying groundwater flow to a canal as a result of the D-F approximation is nearly constant at approximately 25% for ratios greater than 0.5. Bed width to impermeable layer depth ratios for many segments of the San Joaquin River are in the range of 0.5 to 1.0; thus, it is not surprising that our original estimates of groundwater contributions to river flows based on the D-F approximation were consistently low. We also found that the error associated with the D-F approximation in the location of the water table also decreases with an increase in the ratio of canal bed width to depth of the impermeable layer.
Conclusions
The Dupuit-Forchheimer approximation, commonly used in analyzing groundwater flow systems, neglects vertical flows and assumes that the driving force may be represented by the slope of the water table. The approximation is not internally consistent because the result of assuming negligible vertical flow is that the water table has no slope, and thus, no driving force exists (nor groundwater flow). Despite this kind of inconsistency, the D-F approximation greatly simplifies the mathematics and results in errors in the water table position of only a few percent when not in near proximity to water channels. However, in cases of substantial infiltration recharge to the water table and estimation of groundwater flows to relatively wide channels, errors resulting from use of the D-F approximation may be unacceptably large. In the case of estimating groundwater flows to the San Joaquin River, we found that the errors due to the D-F approximation alone may be as large as 25%, compared with estimates not using the approximation. Therefore, the D-F approximation must be used with caution when estimating groundwater flows to channels of substantial width, or located over relatively shallow impermeable layers.